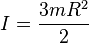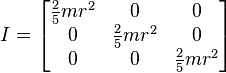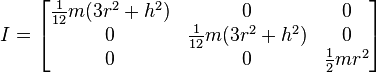Following are scalar moments of inertia. In general, the moment of inertia is a tensor, see below.
Description
Figure
Moment(s) of inertia
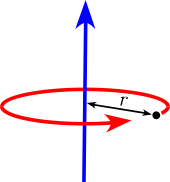
Point mass
m at a distance
r from the axis of rotation. A point mass does not have a moment of inertia around its own axis, but using the
parallel axis theorem a moment of inertia around a distant axis of rotation is achieved.

Two point masses,
M and
m, with
reduced mass μ and separated by a distance,
x.
 Rod
Rod of length
L and mass
m, axis of rotation at the end of the rod. This expression assumes that the rod is an infinitely thin (but rigid) wire. This is also a special case of the thin rectangular plate with axis of rotation at the end of the plate, with
h =
L and
w =
0.

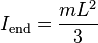 [1]
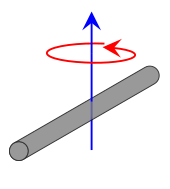
Rod
[1]
Rod of length
L and mass
m. This expression assumes that the rod is an infinitely thin (but rigid) wire. This is a special case of the thin rectangular plate with axis of rotation at the center of the plate, with
w =
L and
h =
0.
 [1]
[1]
Thin circular
hoop of radius
r and mass
m. This is a special case of a
torus for
b = 0 (see below), as well as of a thick-walled cylindrical tube with open ends, with
r1 =
r2 and
h = 0.



Thin, solid
disk of radius
r and mass
m. This is a special case of the solid cylinder, with
h = 0. That

is a consequence of the
Perpendicular axis theorem.
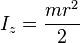

Thin
cylindrical shell with open ends, of radius
r and mass
m. This expression assumes that the shell thickness is negligible. It is a special case of the thick-walled cylindrical tube for
r1 =
r2.
Also, a point mass
m at the end of a rod of length
r has this same moment of inertia and the value
r is called the
radius of gyration.

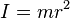 [1]
[1]
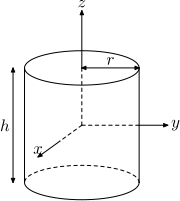
Solid cylinder of radius
r, height
h and mass
m.
This is a special case of the thick-walled cylindrical tube, with
r1 = 0. (Note: X-Y axis should be swapped for a standard right handed frame).

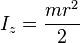 [1]
[1]
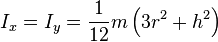
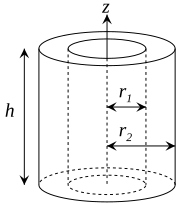
Thick-walled cylindrical tube with open ends, of inner radius
r1, outer radius
r2, length
h and mass
m. With a density of
ρ and the same geometry

,


 [1] [2]
[1] [2]
where
t = (
r2–r1)/
r2 is a normalized thickness ratio;
![I_x = I_y = \frac{1}{12} m\left[3\left({r_2}^2 + {r_1}^2\right)+h^2\right]](http://upload.wikimedia.org/math/3/b/2/3b287e5226f4bb01de7a7a3066f4202a.png) Tetrahedron
Tetrahedron of side
s and mass
m


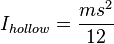 Octahedron
Octahedron (hollow) of side
s and mass
m

 Octahedron
Octahedron (solid) of side
s and mass
m

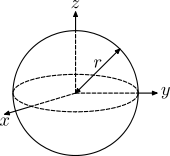
 Sphere
Sphere (hollow) of radius
r and mass
m. A hollow sphere can be taken to be made up of two stacks of infinitesimally thin, circular hoops, where the radius differs from
0 to
r (or a single stack, where the radius differs from
-r to
r).
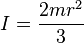 [1]
Ball
[1]
Ball (solid) of radius
r and mass
m. A sphere can be taken to be made up of two stacks of infinitesimally thin, solid discs, where the radius differs from 0 to
r (or a single stack, where the radius differs from
-r to
r).

 [1]
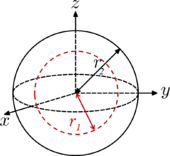
Sphere
[1]
Sphere (shell) of radius
r2, with centered spherical cavity of radius
r1 and mass
m. When the cavity radius
r1 = 0, the object is a solid ball (above).
When
r1 =
r2,
![\left[\frac{{r_2}^5-{r_1}^5}{{r_2}^3-{r_1}^3}\right]=\frac{5}{3}{r_2}^2](http://upload.wikimedia.org/math/d/5/7/d57cd8acd84d2fac233b03050dd61fac.png)
, and the object is a hollow sphere.
![I = \frac{2 m}{5}\left[\frac{{r_2}^5-{r_1}^5}{{r_2}^3-{r_1}^3}\right]\,\!](http://upload.wikimedia.org/math/d/7/3/d7341dbed710e5dd97ef720c6f2582db.png) [1]
Right
[1]
Right circular
cone with radius
r, height
h and mass
m

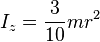 [3]
[3]
 [3]
Torus
[3]
Torus of tube radius
a, cross-sectional radius
b and mass
m.

About the vertical axis:
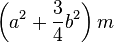 [4]
[4]
About a diameter:
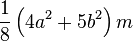 [4]
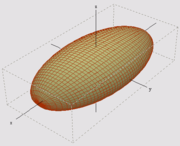
Ellipsoid
[4]
Ellipsoid (solid) of semiaxes
a,
b, and
c with mass
m




Thin rectangular plate of height
h, width
w and mass
m
(Axis of rotation at the end of the plate)


Thin rectangular plate of height
h and of width
w and mass
m

 [1]
[1]
Solid
cuboid of height
h, width
w, and depth
d, and mass
m. For a similarly oriented
cube with sides of length

,
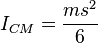

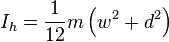
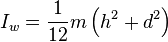
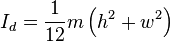
Solid
cuboid of height
D, width
W, and length
L, and mass
m with the longest diagonal as the axis. For a cube with sides

,

.


Triangle with vertices at the origin and at
P and
Q, with mass
m, rotating about an axis perpendicular to the plane and passing through the origin.

Plane
polygon with vertices
P1,
P2,
P3, ...,
PN and mass
m uniformly distributed on its interior, rotating about an axis perpendicular to the plane and passing through the origin.

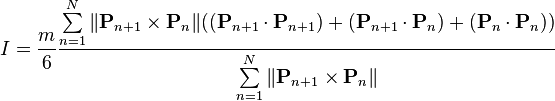
Plane
regular polygon with
n-vertices and mass
m uniformly distributed on its interior, rotating about an axis perpendicular to the plane and passing through the origin.
a stands for side length.
![I=\frac{ma^2}{24}[1 + 3\cot^2(\tfrac{\pi}{n})]](http://upload.wikimedia.org/math/6/c/d/6cd76c9be35e5f277cba4721eacf7606.png) [5]
[5]
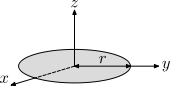
Infinite
disk with mass
normally distributed on two axes around the axis of rotation with mass-density as a function of
x and
y:

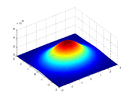

Uniform disk about an axis perpendicular to its edge.
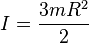 [6]
[6]
List of 3D inertia tensors
This list of
moment of inertia tensors is given for
principal axes of each object.
To obtain the scalar moments of inertia
I above, the tensor moment of inertia
I is projected along some axis defined by a
unit vector n according to the formula:

where the dots indicate
tensor contraction and we have used the
Einstein summation convention. In the above table,
n would be the unit
Cartesian basis ex,
ey,
ez to obtain
Ix,
Iy,
Iz respectively.
Solid
sphere of radius
r and mass
m
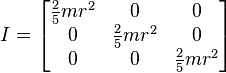
Hollow sphere of radius
r and mass
m


Solid
ellipsoid of semi-axes
a,
b,
c and mass
m
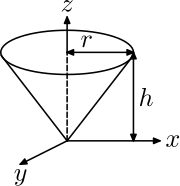
 Right circular cone
Right circular cone with radius
r, height
h and mass
m, about the apex

Solid cuboid of width w, height h, depth d, and mass m

Slender rod along y-axis of length
l and mass
m about end

Slender rod along y-axis of length
l and mass
m about center

Solid cylinder of radius r, height h and mass m
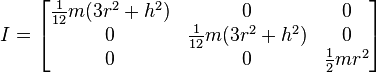
Thick-walled cylindrical tube with open ends, of inner radius
r1, outer radius
r2, length
h and mass
m





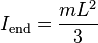





 is a consequence of the
is a consequence of the 
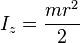


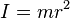

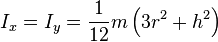
 ,
, 


![I_x = I_y = \frac{1}{12} m\left[3\left({r_2}^2 + {r_1}^2\right)+h^2\right]](http://upload.wikimedia.org/math/3/b/2/3b287e5226f4bb01de7a7a3066f4202a.png)


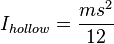




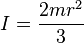


![\left[\frac{{r_2}^5-{r_1}^5}{{r_2}^3-{r_1}^3}\right]=\frac{5}{3}{r_2}^2](http://upload.wikimedia.org/math/d/5/7/d57cd8acd84d2fac233b03050dd61fac.png) , and the object is a hollow sphere.
, and the object is a hollow sphere.
![I = \frac{2 m}{5}\left[\frac{{r_2}^5-{r_1}^5}{{r_2}^3-{r_1}^3}\right]\,\!](http://upload.wikimedia.org/math/d/7/3/d7341dbed710e5dd97ef720c6f2582db.png)

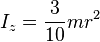


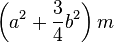
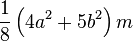








 ,
, 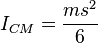

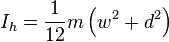
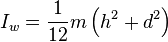
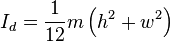
 .
.



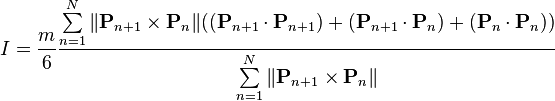
![I=\frac{ma^2}{24}[1 + 3\cot^2(\tfrac{\pi}{n})]](http://upload.wikimedia.org/math/6/c/d/6cd76c9be35e5f277cba4721eacf7606.png)